Сумма внутренних углов многоугольника зависит от количества его сторон. Эта фундаментальная геометрическая закономерность имеет важное значение в планиметрии.
Содержание
Формула суммы внутренних углов
Для выпуклого n-угольника сумма внутренних углов (S) вычисляется по формуле:
| Формула | S = (n - 2) × 180° |
Где n - количество сторон (вершин) многоугольника.
Примеры для различных многоугольников
| Многоугольник | Количество сторон (n) | Сумма углов |
| Треугольник | 3 | (3-2)×180° = 180° |
| Четырехугольник | 4 | (4-2)×180° = 360° |
| Пятиугольник | 5 | (5-2)×180° = 540° |
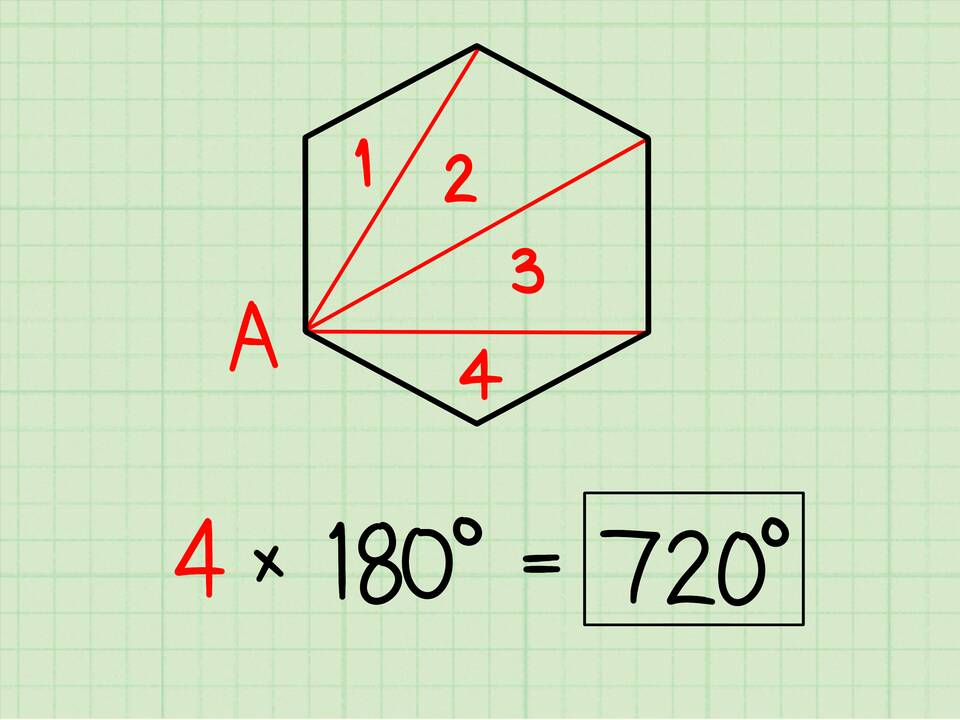
| Шестиугольник | 6 | (6-2)×180° = 720° |
Доказательство формулы
Формула выводится следующим образом:
- Из любой вершины n-угольника проводим все возможные диагонали
- Многоугольник разбивается на (n-2) треугольника
- Сумма углов каждого треугольника равна 180°
- Общая сумма равна произведению количества треугольников на 180°
Особые случаи
- Для правильного многоугольника каждый внутренний угол равен S/n
- Для звездчатых многоугольников формула требует корректировки
- В невыпуклых многоугольниках формула остается верной
Практическое применение
Знание суммы углов многоугольника позволяет:
- Проверять правильность построения фигур
- Решать задачи на построение
- Вычислять неизвестные углы в геометрических фигурах